(34) ソリトン、数値解、厳密解 - 読み書きプログラミング

Korteweg-de Vries方程式を調べます。

$\frac{\partial u}{\partial t}=6u\frac{\partial u}{\partial x}-\frac{\partial^3 u}{\partial x^3}$

これは、非線形微分方程式ですが、可積分であることが知られています。
1ソリトンの厳密解として、以下が知られています。

$u(x,t)=-2\text{sech}^2(x-4t)$

確認してみましょう。

/* 6.2.3m */
u : -2*sech(x - 4*t)^2$
trigsimp(diff(u, t) - 6*u*diff(u, x) + diff(u, x, 3) = 0)$

$0=0$

使用した機能

sech

微分方程式を数値解法で解いた時に何が起こるか見てみます。
単に差分に置き換えた数値解法を試みましょう。
初期条件を $u(x, 0)=-6\text{sech}^2x$ とします。

/* 6.2.6m */
dx : 0.2$
dt : 0.002$
maxGrid : 64$
uPast : makelist(6*sech((k - maxGrid/2)*dx)^2, k, 1, maxGrid)$
uPres : uPast$
gridNumber : makelist(i, i, 1, maxGrid)$

for n : 0 thru 30 do (
  for j : 2 thru maxGrid - 2 do (
    uPres[j] : uPast[j] + dt*(-6*uPast[j]*(uPast[j + 1] - uPast[j])/dx
      - (uPast[j + 2] - 3*uPast[j + 1] + 3*uPast[j] - uPast[j - 1])/(dx^3))
    ),
  plot2d([discrete, gridNumber, uPres], [y, 0, 14])
  )$

発散してしまいました。

微分方程式の対称性を維持する差分近似を導入しましょう。

/* 6.2.9m */
dx : 0.2$
dt : 0.002$
maxGrid : 64$
uPast : makelist(6*sech((k - maxGrid/2)*dx)^2, k, 1, maxGrid)$
uPres : uPast$
uFutu : uPres$
gridNumber : makelist(i, i, 1, maxGrid)$

for n : 0 thru 120 do (
  for j : 3 thru maxGrid - 2 do (
    uPres[j] : uPast[j] + dt*(-6*uPast[j]*(uPast[j + 1] - uPast[j - 1])/(2*dx)
      - (uPast[j + 2] - 2*uPast[j + 1] + 2*uPast[j - 1] - uPast[j - 2])/(2*dx^3))
    ),
  uPast : uPres,
  uPres : uFutu,
  plot2d([discrete, gridNumber, uPres], [y, 0, 14])
  )$

...

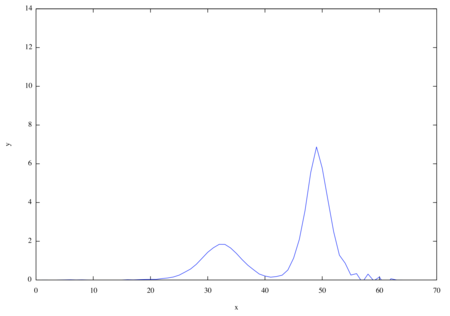
より長期的に解を見ることができました。

初期条件 $u(x, 0)=-6\text{sech}^2x$ の厳密解も知られています。これをプロットしておきましょう。

/* 6.2.10m */
plot3d(12*(4*cosh(2*x-8*t)+cosh(4*x-64*t)+3) / (3*cosh(x-28*t)+cosh(3*x-36*t))^2, [x, -5, 5], [T, -0.2, 0.2], [z,0,9], [grid, 50,50], [gnuplot_pm3d, false], [gnuplot_preamble, "set hidden3d"])$

等高線プロットもしてみましょう。

/* 6.2.11m */
contour_plot((4*cosh(2*x-8*t)+cosh(4*x-64*t)+3) / (3*cosh(x-28*t)+cosh(3*x-36*t))^2, [x, -10, 10], [t, -1, 1], [z, 0, 0.7], [grid, 50, 50], [gnuplot_preamble, "set cntrparam levels auto 14"])$