(47) 能動フィルタを題材とした線形回路分析

能動フィルタのインピーダンスを求めます。
具体例として以下の回路を考えます。

回路図エディタとして、回路シミュレータのPSIMを利用しました。PSIMは素子数と機能が限定されたデモ版がフリーで使うことができます。

PSIMから上記回路のネットリストをファイル名active_filter.cctで保存します。

.TIME 1E-005 0.01 0 1 0 0 0 0 0
R R1 1 2 8k 0 
R R2 3 4 500 0 
R R3 1 5 50 0 
C C1 4 2 0.1u 0 0 
C C2 4 1 0.1u 0 0 
OP_AMP U1 0 2 1 5 -5 
C C3 5 6 1000p 0 0 
OP_AMP U2 6 7 7 5 -5 
C C4 5 7 0.01u 0 0 
R R4 6 0 1k 0 
VP V2 7 
VSIN V1 3 0 220 50 0 0 0

このようなネットリストから、回路が満たすべき制約条件(電流保存、オームの法則などなど)を方程式として出力する解析パッケージを作成しましょう。

/*
 * circuits.mac
 * electric circuit analysis package
 * author: ICHIKAWA, Yuji
 * date: 2011/06/07
 * Copyright (C) 2011 ICHIKAWA, Yuji
 */


kirchhoff_laws(I, net) ::= buildq([I, net],
  block([result : [], net_without_gnd],
    net_without_gnd : rest(net, 1),
    for e in net_without_gnd do (
      result : endcons(lsum(I[i], i, e) = 0, result)),
    return(result)))$


parts_laws(V, I, parts, net) ::= buildq([V, I, parts, net],
  block([result : [V[1] = 0]], /* Ground voltage = 0 */
    for e in parts do (
      if e[kind_index] = VP then
      /* Probes should have infinite impedance. */
      result : endcons(I[e[terminal_index][1]] = 0, result)
      elseif member(e[kind_index], two_terminal_parts)
      then block([nodes, Z],
        result : endcons(lsum(I[i], i, e[terminal_index]) = 0, result),
        nodes : terminals_to_nodes(e[terminal_index], net),
        if e[kind_index] = VSIN
        then result : endcons(V[nodes[1]] - V[nodes[2]] = 1, result)
        else (
          Z : if e[kind_index] = R then e[symbol_index]
          elseif e[kind_index] = C then 1/(%i*omega*e[symbol_index])
          elseif e[kind_index] = L then %i*omega*e[symbol_index],
          result : endcons(V[nodes[1]] - V[nodes[2]] = Z*I[e[terminal_index][1]], result)))
      elseif e[kind_index] = OP_AMP
      then block([nodes],
        result : append(result, [I[e[terminal_index][1]] = 0, I[e[terminal_index][2]] = 0]),
        nodes : terminals_to_nodes(e[terminal_index], net),
        result : endcons(V[nodes[1]] = V[nodes[2]], result))),
    return(result)))$


load_netlist(file) := block([fs, parts : [], n, nodes, line, terminal : 0],
  fs : openr(file),
  n : length(node_list(fs)),
  close(fs),
  nodes : makelist([], i, 1, n),
  fs : openr(file),
  while (line : readline(fs)) # false do block([pl],
    pl : parse_line(line),
    if pl # [] then block([terminals : []],
      for i in pl[terminal_index] do (
        terminal : terminal + 1,
        nodes[i + 1] : endcons(terminal, nodes[i + 1]),
        terminals : endcons(terminal, terminals)
        ),
      pl[terminal_index] : terminals,
      parts : endcons(pl, parts))),
  close(fs),
  return([terminal, parts, nodes]))$


/* functions for internal use */

/* PSIM netlist (.cct) constants */
node_index : 3 $

/* parts list constants */
terminal_index : 3 $

/* common parts list constants */
symbol_index : 2 $
kind_index : 1 $


two_terminal_parts : [R, C, L, VSIN]$
three_terminal_parts : [OP_AMP]$
one_terminal_parts : [VP]$

number_of_terminals(kind) := 
  if member(kind, two_terminal_parts) then 2
  elseif member(kind, three_terminal_parts) then 3
  elseif member(kind, one_terminal_parts) then 1
  else error("unknown part")$

value_index(kind) := node_index + number_of_terminals(kind)$

/* example: [R, R1, [0, 1], [1e3]] */
parse_line(str) := block([ts, result : [], value_i],
  ts : tokens(str),
  if charat(ts[kind_index], 1) = "." then return([]),
  for i : 1 thru symbol_index do
    result : endcons(parse_string(ts[i]), result),
  value_i : value_index(result[kind_index]),
  result : endcons(makelist(parse_string(ts[i]), i, node_index, value_i - 1), result),
  result : endcons(makelist(prefix_to_number(ts[i]), i, value_i, length(ts)), result),
  return(result))$

/* transform prefix of unit to number */
prefix_to_number(str) := block([last_char : charat(str,slength(str))],
  if digitcharp(last_char) then parse_string(str)
  else
    parse_string(substring(str, 1, slength(str))) *
    assoc(last_char, ["k"=1e3, "m"=1e-3, "u"=1e-6, "n"=1e-9, "p"=1e-12], 1))$

node_list(file_stream) := block([nodes : {}, line],
  while (line : readline(file_stream)) # false do block([ts],
    ts : parse_line(line),
    if ts # [] then nodes : union(setify(ts[node_index]), nodes)),
  return (listify(nodes)))$

terminals_to_nodes(terminals, net) := block([result : []],
  for e in terminals do (
    for i : 1 thru length(net) do (
      if member(e, net[i]) then (result : endcons(i, result), return()))),
  return(result))$

使用した機能

load_netlistは、PSIMのネットリストファイルを読み込み、通しの端子番号を生成して、総端子数と解析用の部品リスト、ネットリストを返します。
kirchhoff_lawsは、Kirchhoffの法則に基づく方程式をネットリストから生成します。
parts_lawsは、Ohmの法則などに基づく部品が満たすべき方程式を部品リスト、ネットリストから生成します。

では、具体例を解かしてみましょう。

/* 8.1.9m */
load("circuits")$

[t, parts, net] : load_netlist("active_filter.cct");

eqns : append(kirchhoff_laws(I, net), parts_laws(V, I, parts, net));
sol : solve(eqns, append(makelist(V[i], i, 1, length(net)), makelist(I[i], i, 1, t)))$
V[8], sol;

$\begin{align*} &[25,[[R,R1,[1,2],[8000.0,0]],[R,R2,[3,4],[500,0]],[R,R3,[5,6],[50,0]],[C,C1,[7,8],[1.\,{10}^{-7},0,0]],[C,C2,[9,10],[1.\,{10}^{-7},0,0]],[OP\_AMP,U1,[11,12,13],[5,-5]],[C,C3,[14,15],[1.\,{10}^{-9},0,0]],[OP\_AMP,U2,[16,17,18],[5,-5]],[C,C4,[19,20],[1.\,{10}^{-8},0,0]],[R,R4,[21,22],[1000.0,0]],[VP,V2,[23],[]],[VSIN,V1,[24,25],[220,50,0,0,0]]],\\ &[[11,22,25],[1,5,10,13],[2,8,12],[3,24],[4,7,9],[6,14,19],[15,16,21],[17,18,20,23]]] \end{align*}$

$\begin{align*} [{I}_{13}+{I}_{10}+{I}_{5}+{I}_{1}&=0,\\ {I}_{12}+{I}_{8}+{I}_{2}&=0,\\ {I}_{24}+{I}_{3}&=0,\\ {I}_{9}+{I}_{7}+{I}_{4}&=0,\\ {I}_{19}+{I}_{14}+{I}_{6}&=0,\\ {I}_{21}+{I}_{16}+{I}_{15}&=0,\\ {I}_{23}+{I}_{20}+{I}_{18}+{I}_{17}&=0,\\ {V}_{1}&=0,\\ {I}_{2}+{I}_{1}&=0,\\ {V}_{2}-{V}_{3}&={I}_{1}\,R1,\\ {I}_{4}+{I}_{3}&=0,\\ {V}_{4}-{V}_{5}&={I}_{3}\,R2,\\ {I}_{6}+{I}_{5}&=0,\\ {V}_{2}-{V}_{6}&={I}_{5}\,R3,\\ {I}_{8}+{I}_{7}&=0,\\ {V}_{5}-{V}_{3}&=-\frac{i\,{I}_{7}}{\omega\,C1},\\ {I}_{10}+{I}_{9}&=0,\\ {V}_{5}-{V}_{2}&=-\frac{i\,{I}_{9}}{\omega\,C2},\\ {I}_{11}&=0,\\ {I}_{12}&=0,\\ {V}_{1}&={V}_{3},\\ {I}_{15}+{I}_{14}&=0,\\ {V}_{6}-{V}_{7}&=-\frac{i\,{I}_{14}}{\omega\,C3},\\ {I}_{16}&=0,\\ {I}_{17}&=0,\\ {V}_{7}&={V}_{8},\\ {I}_{20}+{I}_{19}&=0,\\ {V}_{6}-{V}_{8}&=-\frac{i\,{I}_{19}}{\omega\,C4},\\ {I}_{22}+{I}_{21}&=0,\\ {V}_{7}-{V}_{1}&={I}_{21}\,R4,\\ {I}_{23}&=0,\\ {I}_{25}+{I}_{24}&=0,\\ {V}_{4}-{V}_{1}&=1] \end{align*}$

$-{{\omega^2\,{\it C_1}\,{\it C_3}\,{\it R_1}\,{\it R_4}}\over{ {\it R_1}\,{\it R_2}\,\left({\it C_1}\,\left(i\,\omega^3\,{\it C_2} \,{\it C_3}\,{\it R_4}+\omega^2\,{\it C_2}\right)+i\,\omega^3\, {\it C_1}\,{\it C_2}\,\left({\it C_4}+{\it C_3}\right)\,{\it R_3} \right)+{\it R_2}\,\left({\it C_1}\,\left(\omega^2\,{\it C_3}\, {\it R_4}-i\,\omega\right)+\omega^2\,{\it C_2}\,{\it C_3}\,{\it R_4} +\left(\omega^2\,{\it C_2}\,\left({\it C_4}+{\it C_3}\right)+\omega^ 2\,{\it C_1}\,\left({\it C_4}+{\it C_3}\right)\right)\,{\it R_3}-i\, \omega\,{\it C_2}\right)-i\,\omega\,{\it C_3}\,{\it R_4}+i\,\omega\, \left(-{\it C_4}-{\it C_3}\right)\,{\it R_3}-1}}$

わかりにくいので、具体的な回路パラメータを入れてみましょう。

/* 8.1.10m */
v8s : ratsimp(V[8]), solutions, R1 = 8000, R2 = 500, R3 = 50, R4 = 1000, C1 = 10^(-7), C2 = 10^(-7), C3 = 10^(-9), C4 = 10^(-8);

$-\frac{400000\,{\omega}^{2}}{31\,i\,{\omega}^{3}+20077500\,{\omega}^{2}-50775000000\,i\,\omega-500000000000000}$

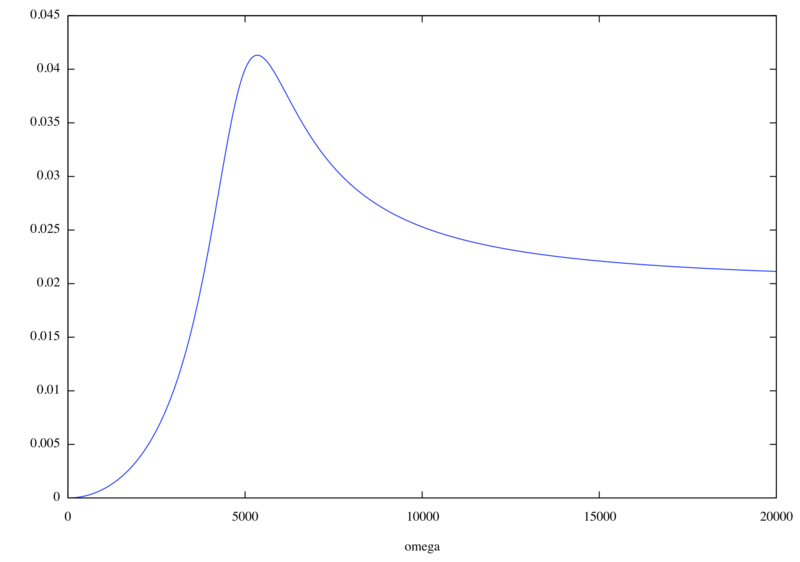
このゲインをプロットしてみましょう。

plot2d(cabs(v8s), [omega, 0, 20000]);

参考文献

Crandall, Mathematica―理工系ツールとしての (アジソンウェスレイ・トッパン情報科学シリーズ) p.229-p.234

使用ツール

Powersim社, 回路シミュレータPSIM

読み書きプログラミング

日常のプログラミングで気づいたことを綴っています

(47) 能動フィルタを題材とした線形回路分析

使用した機能

参考文献

使用ツール