水素原子のSchrödinger方程式は厳密解が知られていますが、より複雑な分子を検討する際の足場として数値解法を見ておくことは有意義です。
ここでは、角運動量が0の時の水素原子のSchrödinger方程式を有限要素法で解きます。対象となる微分方程式は、以下のものです。
rに関して、間隔εでn+1個のノードに離散化します。ノード間の間の波動関数の値はノードの値の線形近似で内挿します。
線形近似なのでノードで微分が不連続になり、二階微分は発散します。二階微分を避けるため、対象の方程式を積分方程式に変形します。具体的には、を掛けて積分し、部分積分します。すると、次の式を得ます。
この式は、離散化した波動関数で計算することができ、結果は、Eとが満たすべき行列方程式です。
これをMaximaに解かせましょう。
/* 7.2.6m */ load("lapack")$ load("eigensys")$ eps : 0.5$ n : 40$ h11[m] := eps*(m^2 - m + 1/3) + eps^2*(1/2 - 2*m/3)$ h12[m] := -eps*(m^2 - m + 1/3) + eps^2*(1/6 - m/3)$ h22[m] := eps*(m^2 - m + 1/3) + eps^2*(1/6 - 2*m/3)$ u11[m] := eps^3*(m^2/3 - m/2 + 1/5)$ u12[m] := eps^3*(m^2/6 - m/6 + 1/20)$ u22[m] := eps^3*(m^2/3 - m/6 + 1/30)$ hterm[a, b] := ( if a = b then if a = 1 then h11[a] elseif a = n + 1 then h22[a - 1] else h22[a - 1] + h11[a] elseif abs(a - b) = 1 then h12[min(a, b)] else 0 )$ uterm[a, b] := ( if a = b then if a = 1 then u11[a] elseif a = n + 1 then u22[a - 1] else u22[a - 1] + u11[a] elseif abs(a - b) = 1 then u12[min(a, b)] else 0 )$ h : genmatrix(hterm, n + 1, n + 1)$ u : genmatrix(uterm, n + 1, n + 1)$ v : invert_by_lu(u) . h$ [energies, wavefunctions, dummy] : dgeev(v, true, false)$ wavefunctions : transpose(wavefunctions)$ for k : 1 thru n + 1 do ( if energies[k] < 0 then ( print("E_", k, " = ", energies[k]), plot2d([discrete, makelist(i, i, 1, length(wavefunctions[k])), wavefunctions[k]]) ) )$
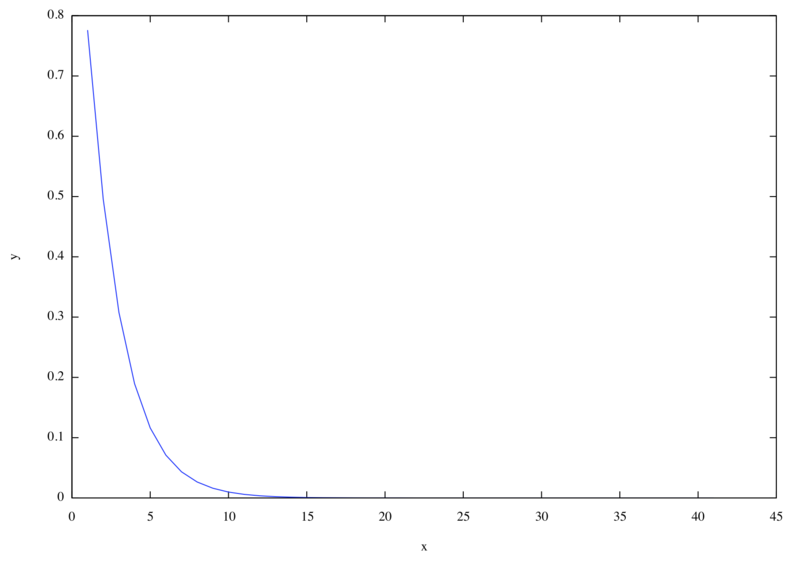
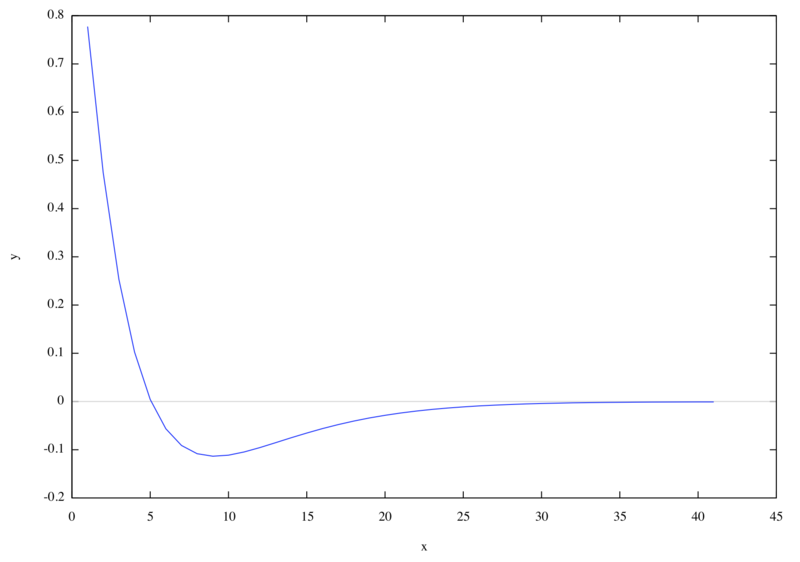
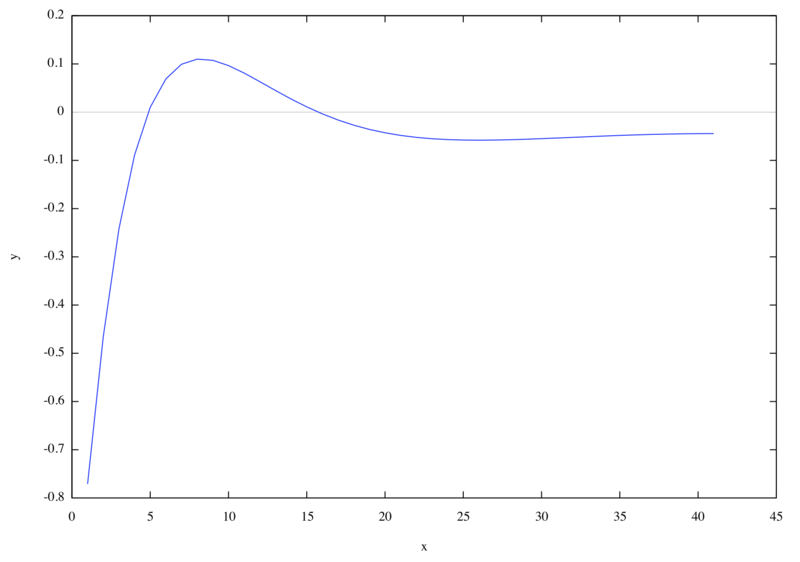

使用した機能
参考文献
- Crandall, Mathematica―理工系ツールとしての (アジソン ウェスレイ・トッパン情報科学シリーズ) p.194-p.200