(38) Sierpinski三角形 - 読み書きプログラミング

自己相似な三角形であるSierpinski三角形は、色々な方法で生成することができます。
ここでは、カオスゲーム(ランダム反復函数系)を使ってみます。
ある点に対して、ランダムに(0, 0), (1, 0), (0, 1)のいずれかを選び、ある点と選ばれた点の中点を与える写像を考えます。ある初期値(ここでは(0.7, 0.4))から始め、この写像の繰り返しの軌跡の再近接格子点を集めると、Sierpinski三角形が出来上がります。

描画してみましょう。

/* 6.3.10m */
aging : 1000$
grid : 200$
m : 0.7$
n : 0.4$
lis : [];
for i : 1 thru grid*grid/2 + aging do (
  if i > aging then (
    mm : round(grid*m)/grid,
    nn : round(grid*n)/grid,
    if not member([mm, nn], lis) then lis : endcons([mm, nn], lis)
    ),
  q : random(3),
  if q = 0 then (
    m : m/2,
    n : n/2
    )
  elseif q = 1 then (
    m : m/2,
    n : (1 + n)/2
    )
  else (
    m : (1 + m)/2,
    n : n/2
    )
  )$
print(length(lis))$
plot2d([discrete, lis], [style, dots]);

$6131$

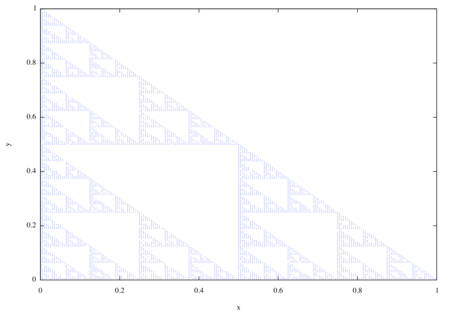
描画に使う格子点の数Nとグリッド長Lの関係がSierpinski三角形のフラクタル次元を示します。具体的には、

$d=\frac{\log N}{\log L}$

で次元が与えられます。

Sierpinski三角形のフラクタル次元を算出してみましょう。

/* 6.3.14m */
aging : 1000$
for grid : 10 step 10 thru 60 do (
  m : 0.7,
  n : 0.4,
  lis : [],
  for i : 1 thru grid*grid/2 + aging do (
    if i > aging then (
      mm : round(grid*m)/grid,
      nn : round(grid*n)/grid,
      if not member([mm, nn], lis) then lis : endcons([mm, nn], lis)
      ),
    q : random(3),
    if q = 0 then (
      m : m/2,
      n : n/2
      )
    elseif q = 1 then (
      m : m/2,
      n : (1 + n)/2
      )
    else (
      m : (1 + m)/2,
      n : n/2
      )
    ),
  print(grid, " ", length(lis), " ", float(log(length(lis))/log(grid)))
  )$