(35) N-ソリトン解 - 読み書きプログラミング

KdV方程式の続きです。
KdV方程式の初期条件をポテンシャルとする定常Schrödinger方程式を解くと、KdV方程式の厳密解が求められることが知られています。
初期条件に以下を仮定します。

$u(x, 0)=-N(N+1)\text{sech}^2x$

これをポテンシャルとする定常Schrödinger方程式の解は以下になります。

$\Psi_m(x)=c_mP^m_N(\tanh x)$

$P^m_N$ はLegendreの陪函数であり、 $c_m$ は規格化係数です。

n=4について、規格化された定常解の関数を定義しておきましょう。1つだけ波形も見ておきましょう。

/* 6.2.19m */
n : 4$
f(x, m) := assoc_legendre_p(n, m, tanh(x))$
norm(m) := sqrt(integrate(f(x, m)^2, x, -inf, inf))$
Psi(x, m) := f(x, m) / norm(m)$
plot2d(Psi(x, 1), [x, -7.5, 7.5])$

使用した機能

規格化係数を求めておきましょう。

/* 6.2.20m */
for j : 1 thru n do (
  c[j] : limit(trigexpand(Psi(x, j)*%e^(j*x)), x, inf),
  print(c[j]))$

$-2\,\sqrt{5}$

$6\,\sqrt{5}$

$-2\,\sqrt{105}$

$2\,\sqrt{70}$

使用した機能

trigexpand

厳密解を求めるために、行列を定義します。

$A_{ij}=\delta_{ij}+\frac{c_i^2}{i+j}e^{8i^3t-(i+j)x}$

すると、KdV方程式の厳密解が以下で与えられます。

$u(x,t)=-2\frac{\partial^2}{\partial x^2}\log\det A$

n=4の時の厳密解を計算しましょう。

/* 6.2.21m, 6.2.22m */
a : ident(n) + genmatrix(e, n, n), e[i, j] := c[i]^2/(i + j)*exp(8*i^3*t - (i + j)* x)$
d : determinant(a), expand;
u : -2*diff(diff(d, x)/d, x);

$10\,{e}^{8\,t-2\,x}+45\,{e}^{64\,t-4\,x}+70\,{e}^{216\,t-6\,x}+50\,{e}^{72\,t-6\,x}+35\,{e}^{512\,t-8\,x}+175\,{e}^{224\,t-8\,x}+126\,{e}^{520\,t-10\,x}+126\,{e}^{280\,t-10\,x}+175\,{e}^{576\,t-12\,x}+35\,{e}^{288\,t-12\,x}+50\,{e}^{728\,t-14\,x}+70\,{e}^{584\,t-14\,x}+45\,{e}^{736\,t-16\,x}+10\,{e}^{792\,t-18\,x}+{e}^{800\,t-20\,x}+1$

$\-2\,\left({{40\,e^{8\,t-2\,x}+720\,e^{64\,t-4\,x}+2520\,e^{216\,t-6 \,x}+1800\,e^{72\,t-6\,x}+2240\,e^{512\,t-8\,x}+11200\,e^{224\,t-8\, x}+12600\,e^{520\,t-10\,x}+12600\,e^{280\,t-10\,x}+25200\,e^{576\,t- 12\,x}+5040\,e^{288\,t-12\,x}+9800\,e^{728\,t-14\,x}+13720\,e^{584\, t-14\,x}+11520\,e^{736\,t-16\,x}+3240\,e^{792\,t-18\,x}+400\,e^{800 \,t-20\,x}}\over{10\,e^{8\,t-2\,x}+45\,e^{64\,t-4\,x}+70\,e^{216\,t- 6\,x}+50\,e^{72\,t-6\,x}+35\,e^{512\,t-8\,x}+175\,e^{224\,t-8\,x}+ 126\,e^{520\,t-10\,x}+126\,e^{280\,t-10\,x}+175\,e^{576\,t-12\,x}+35 \,e^{288\,t-12\,x}+50\,e^{728\,t-14\,x}+70\,e^{584\,t-14\,x}+45\,e^{ 736\,t-16\,x}+10\,e^{792\,t-18\,x}+e^{800\,t-20\,x}+1}}-{{\left(-20 \,e^{8\,t-2\,x}-180\,e^{64\,t-4\,x}-420\,e^{216\,t-6\,x}-300\,e^{72 \,t-6\,x}-280\,e^{512\,t-8\,x}-1400\,e^{224\,t-8\,x}-1260\,e^{520\,t -10\,x}-1260\,e^{280\,t-10\,x}-2100\,e^{576\,t-12\,x}-420\,e^{288\,t -12\,x}-700\,e^{728\,t-14\,x}-980\,e^{584\,t-14\,x}-720\,e^{736\,t- 16\,x}-180\,e^{792\,t-18\,x}-20\,e^{800\,t-20\,x}\right)^2}\over{ \left(10\,e^{8\,t-2\,x}+45\,e^{64\,t-4\,x}+70\,e^{216\,t-6\,x}+50\,e ^{72\,t-6\,x}+35\,e^{512\,t-8\,x}+175\,e^{224\,t-8\,x}+126\,e^{520\, t-10\,x}+126\,e^{280\,t-10\,x}+175\,e^{576\,t-12\,x}+35\,e^{288\,t- 12\,x}+50\,e^{728\,t-14\,x}+70\,e^{584\,t-14\,x}+45\,e^{736\,t-16\,x }+10\,e^{792\,t-18\,x}+e^{800\,t-20\,x}+1\right)^2}}\right)$

使用した機能

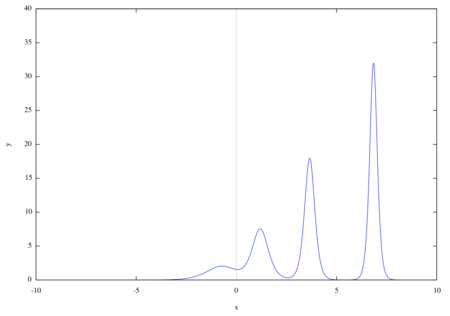
では、計算した厳密解をプロットしてみましょう。

for t : -0.15 step 0.05 thru 0.15 do plot2d(-u, [x, -10, 10], [y, 0, 2*(n^2+n)])$

...

参考文献

Crandall, Mathematica―理工系ツールとしての (アジソンウェスレイ・トッパン情報科学シリーズ) p.164-p.171